Try IT(トライイット)の関数y=ax^2の勉強法の映像授業ページです。 Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。 二次関数 y = ax2 bx c y = a x 2 b x c のグラフをかくためには、まず頂点を求める必要がありました。 つまり、 y = a(x−p)2 q y = a ( x − p) 2 q の形に式変形をする必要がある、ということです。 このような式変形を行うことを「 平方完成 する」というん『 y は x の2乗に比例する y = ax ²』

yはxの二乗に比例する関数の問題 y ax 2とおこう 中学や高校の数学の計算問題
Y=ax二乗+bx+c 符号
Y=ax二乗+bx+c 符号-関数 y=ax 2 のグラフ(1) 関数 y=ax 2 のグラフ(2) 関数 y=ax 2 のグラフ(3) 関数 y=ax 2 のグラフ(4) 変域とグラフ(1) 変域とグラフ(2) 変域の割合(1) 変域の割合(2) 変域の割合(3) 変化の割合とグラフ 直線と放物線(1) 直線と放物線(2) 直線と放物線(3) 関数 y=ax 2 の活用(1) 関数 y=ax 2 の活用(2) 関数 y=ax 2 の活用(3) 関数 y=ax 2 の活用(4) 5最小二乗法に関するメモ 千葉豪 19年10月25日 1 基本的な考え方 11 基本中の基本 あるパラメータxに依存して決まるパラメータy があるとして1、このふたつのパラメータにつ いてy = ax b なる関係があるとする。 測定により、I 個の異なるx の値に対してy の値が得ら れたものとし、そのセット
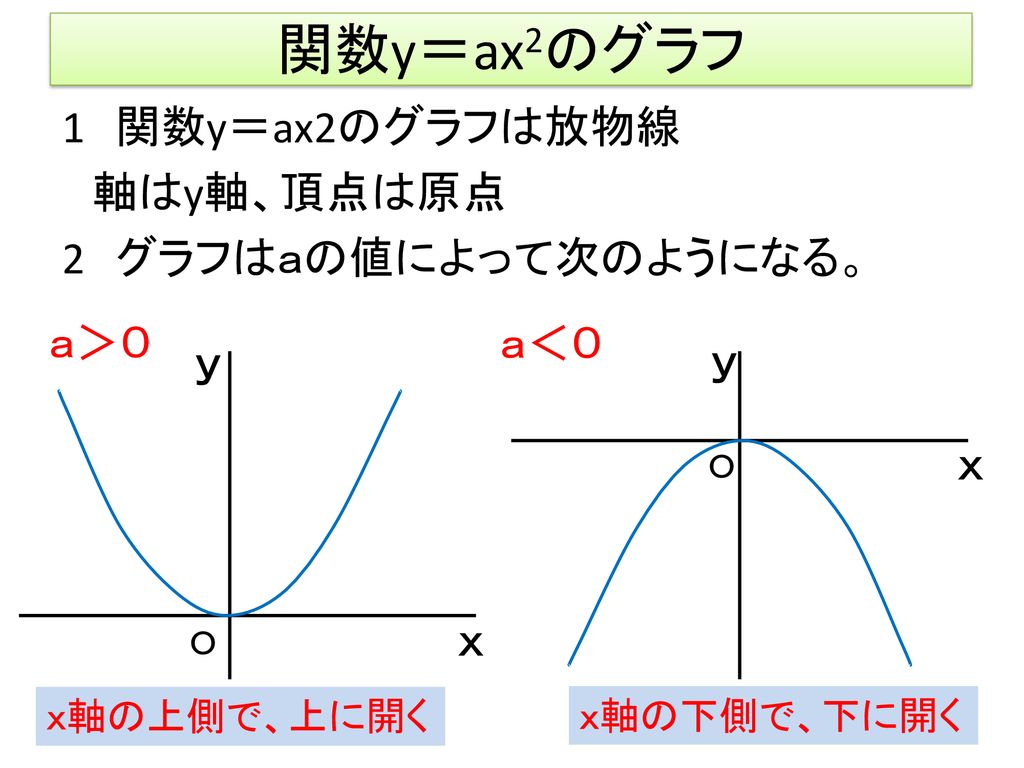



ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download
Y=ax 2 bxc(2次曲線)の場合 データ列(x,y)が与えられたとき,以下のEを最小化してa,b,cを求める問題を考えよう. Eをa,b,cそれぞれで偏微分して=0とおいて得られる連立方程式は,回帰分析と相関係数 1 回帰分析 下図のように(x,y) のデータをプロットしたとき,x,y に比例関係が成り立ちそうな場合がある. このデータにぴったり当てはまる直線の式y = ax b を決定するのに最小二乗法が適用できる.こ のような,二つの変数の間の関係式を求める分析を回帰分析と呼んで最小二乗基準 y y = a x b 多数の点のデータから直線の数式 表現(すなわちa とb )を求める。 x 最小二乗基準 y= ax
y=ax^2bxcの変形について教えてください!y=2x^28x11 =2(x^24x)11 =2{(x2)^22^2}11 ↑このマイナス2の2乗ってどのからきたのですか?2{ のとこの2を引いてるんですか?でもなんで二乗がつくのか分かり 最小二乗法y=axbのa,b導出方法についてメモする 統計 ☆こんてんつ 回帰分析で用いる、最小二乗法の原理をメモする。 どのようにして添え字の量(回帰係数)が導出されるかを記載。 回帰方程式 回帰係数の決定 ★回帰方程式 x を食べる量、 y を体重最小二乗フィット:直線モデルの例問題の設定 00 000 0 (),, () ii ii i xy x y yx ax b ab ab yx ax b yyx σ = = 測定値の組( , )があり、独立変数と従属変数の間の関係を で近似するとき 、 に関する最も確からしい推定値は どうやって決められるか?
関数 関数y =ax2(2) 1 次の各問いに答えなさい。 (1)yはxの2乗に比例し、x=3 のときy =27 である。 ① yをxの式で表しなさい。 ② x=5 のときのyの値を求めなさい。 (2)関数y = ax2で,x=2 のときy = −8である。 ① aの値を求めなさい。 ② x= −4のときのyの値を求めなさい。 (3)yはxの2乗に比例Y=ax2について理解するとともに,関数関係を見いだし表現し考察する能力を伸ばす。 ① 事象の中には関数y=ax 2 としてとらえられるものがあることを理解することができる。最小二乗法 擬似逆行列 下のサイトの説明を読んで最小二乗法の勉強をしています。 未知パラメータxが1個(N=1)、出力yが10個(M=10)のとき、 擬似逆行列を求めようとすると、(A#A)^1 が1×1行列になってしまいます。




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく
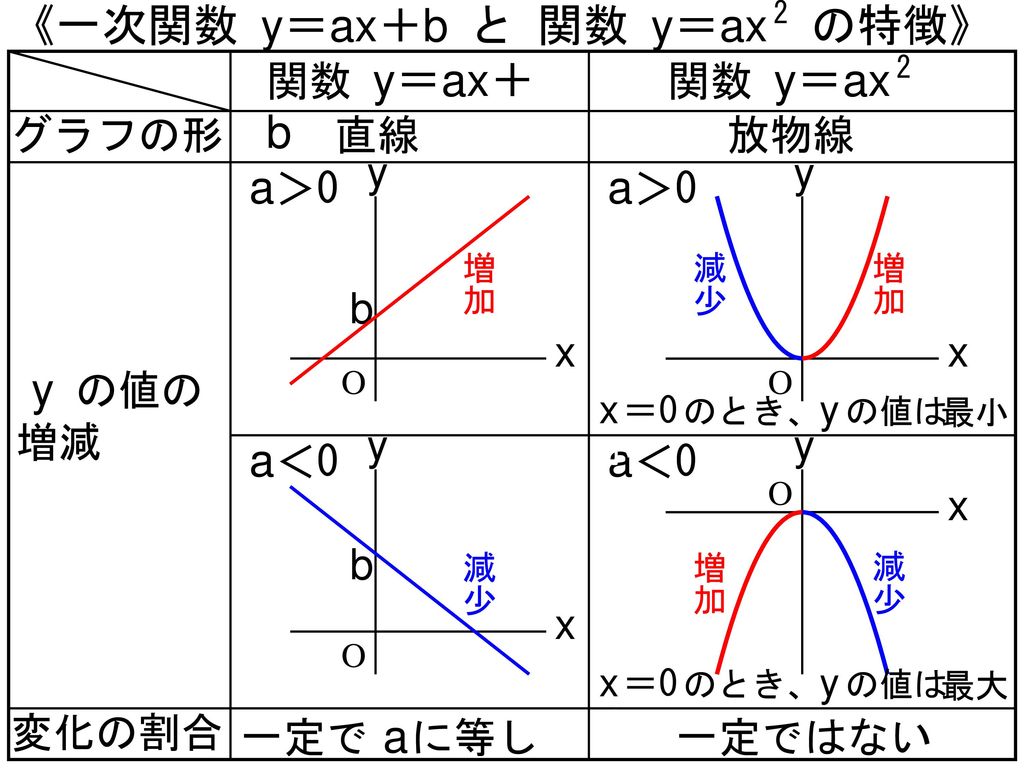



4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download
というデータが与えられたとき、これを直線y = axb で近似するにはどのようにa とb を決めれば良いかとい う問題である。 a とb を決めたとき、データ点を(xi;yi);i = 1;;n のとき、データ点と直線とのズレ(誤差)の二乗の和を 計算すると、 E(a;b) = ∑n i=1 (yi求める直線の方程式をy=axbとします。 このときaの値は a=yの増加量÷xの増加量 で求めることができます。 (ここがわからない場合は、 変化の割合 を復習してみましょう) yの増加量=4-2=2 xの増加量=2-1=1 よってa=2÷1=2となり、直線の方程式Y = a x 2 の関係にある2量に着目し、関数的な考え方を進んで活用しようとする 式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味
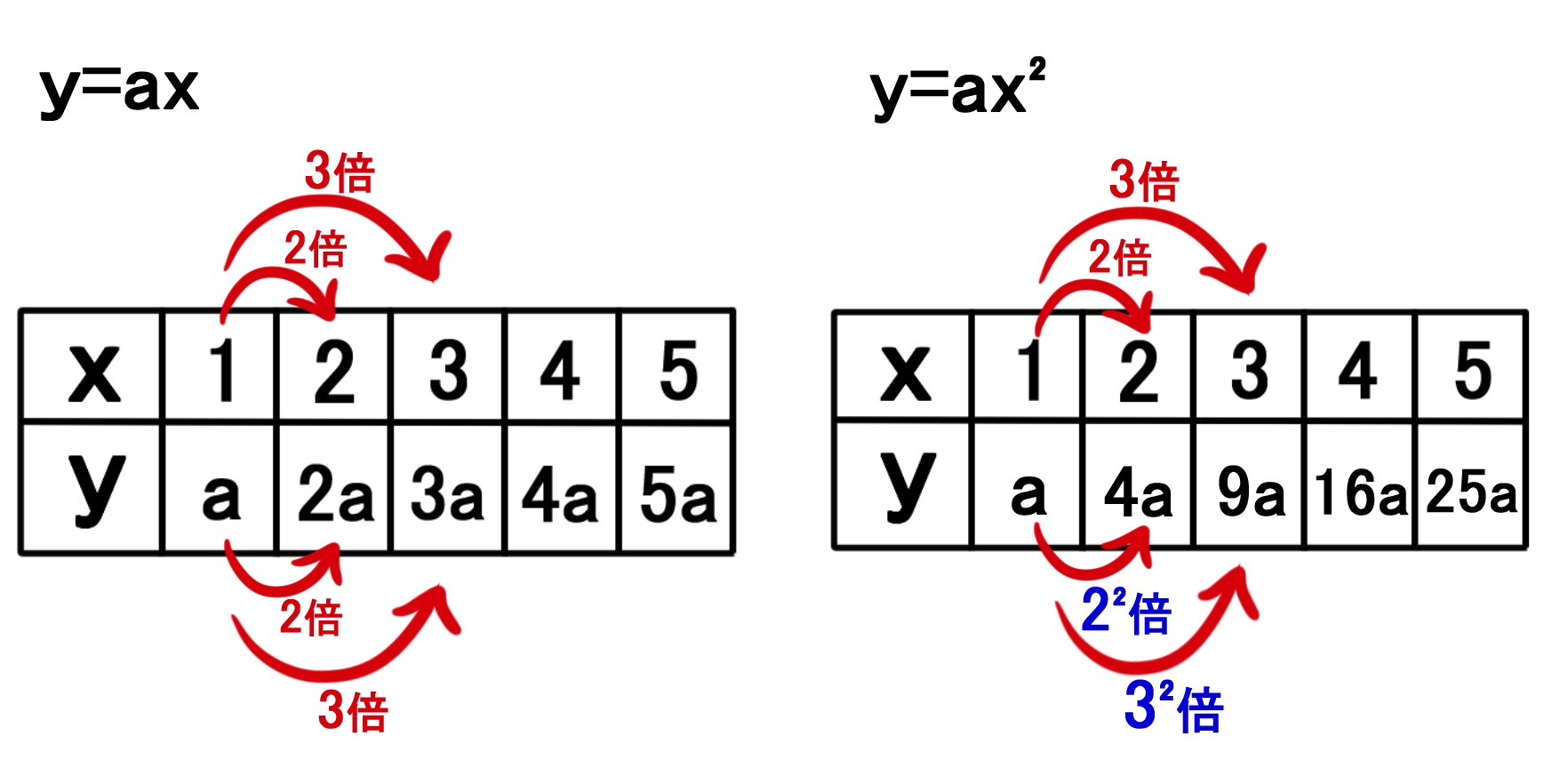



バカでもわかる 中学数学




二次関数y Ax2の比例定数の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
補間法と最小二乗法(2) 最小二乗法 今回はデータ処理の一つの要である最小二乗法について学ぶ. 2つの変数間の関係が理論的に判っているものを実験などで計測し,その係数を求めたい場合がある.(例えば比例関係となるばね係数や,1次遅れ系の時定数など)最小二乗法 データ点の列{𝑥𝑥 𝑘𝑘,𝑦𝑦 𝑘𝑘}(𝑘𝑘= 0,⋯𝑛𝑛−1) どのような関数形かを推定 予想する関数形𝑦𝑦= 𝑓𝑓𝑥𝑥 パラメタを含む 二乗誤差を最小化 2 (( )) 1 0 min 2 k n k k y f x − = − ∑Y=ax2乗の利用① 平均の速さ等 中3数学 関数y=ax二乗 5 y=ax2乗の利用① 平均の速さ等 中3数学 関数y=ax二乗 5 Watch later Share Copy link Info



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf




2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張
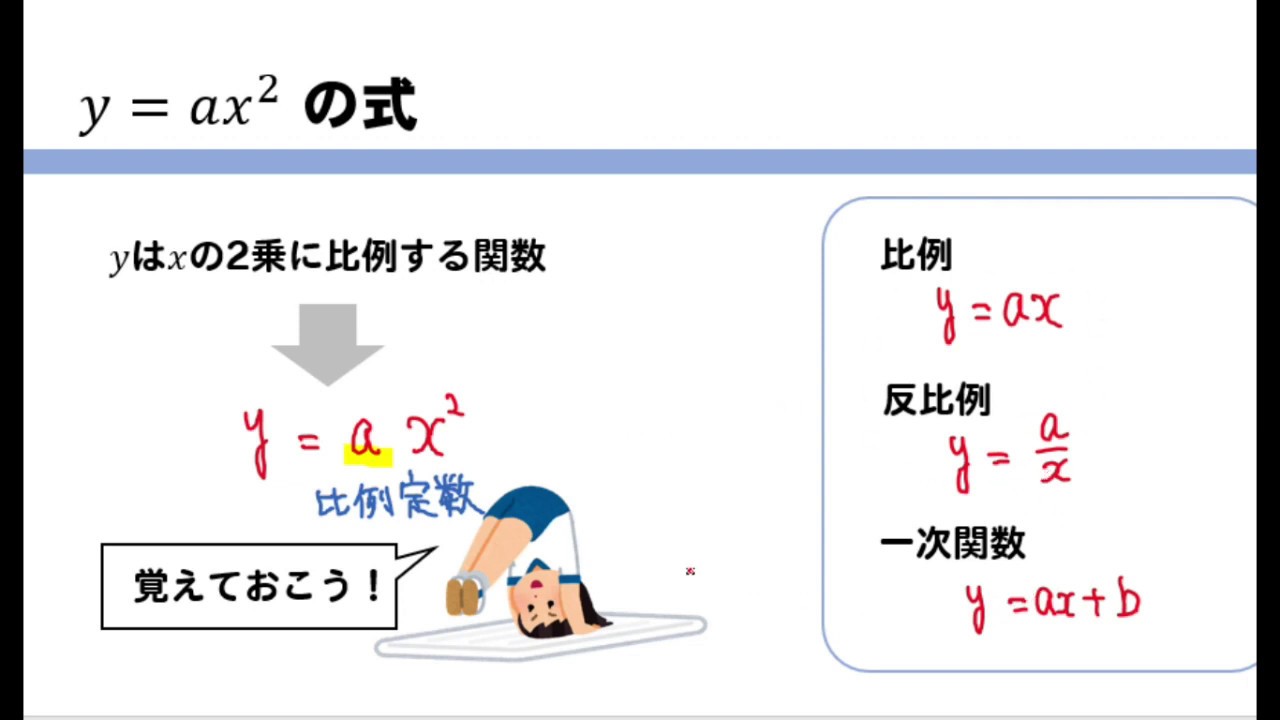
6 回帰分析、最小二乗法1 線形回帰分析(2変数) 2 つの変数y とx の間には次の関係があるとしよう。 y = α β x ε この時y は被説明変数( もしくは従属変数)、 x は説明変数(もしくは独立変数)、εを誤差項という。 ε はx が説明しきれない部分をまとめたものであり、 e(ε) = 0 の確率変数であるとYの変域が0からプラスになっているので,y=ax 2 は上に開いている放物線 (a>0)だということを確認しましょう。 次に,xの変域が2≦x≦4なので, 2≦x≦0の範囲では,関数y=ax 2 は減少する一方で, 0≦x≦4の範囲では,関数y=ax 2 は増加する一方です。Y = ax2 y = a x 2 2乗に比例 y y が x x の関数であり、 x x と y y の間に y = ax2 y = a x 2 という関係式が成り立つとき、 y y は x x の 2 2 乗に比例する という。 ただし、 a a は 0 0 でない定数で、比例定数といいます。 「 y y は x x の 2 2 乗に比例する」と問題文に




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



Y Ax の式を求める 変域から Youtube
最小二乗法とは, データの組 (x i, y i) (x_i,y_i) (x i , y i ) が多数与えられたときに, x x x と y y y の関係を表す もっともらしい関数 y = f (x) y=f(x) y = f (x) を求める方法です。入力x,出力yとが直線関係にあれば次式で表される。 ここで, a, b は任意の定数である。 n 組の測定データ: 最も良く当てはまる直線は, y i と ax i b との差の2乗の和が 最小となる a と b の場合である。 y ax b 2)最小二乗法の計算 1 1 2 2 x y x yこのページでは、中学校学習レベルの数式を英語で読む方法をご説明しています。 2次方程式 $ ax^2bxc=0 $ や、その解の公式 $ x=\frac{b \pm \sqrt{b^2 4ac}}{2a} $ のような文字式、ルート、累乗を含む式って英語でなんて言えばいいんだろう そんな疑問をこのページで解決しましょう!



2次関数の各係数の意味
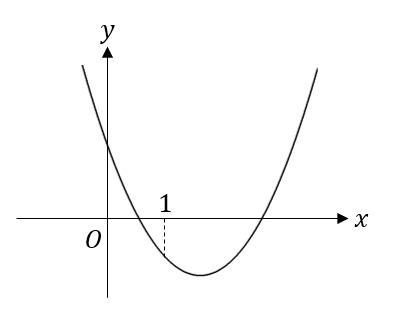



二次関数 係数の符号の決定 グラフから符号を決めるポイントを解説 数スタ
「yはxの2乗に比例する」 というのは、 y=ax 2 と表せる、ということがポイントなんだ。つまり、測定値(xi,yi)と求めた直線(曲線)から計算した値との差が最も小 さくなるように、係数を決める方法である。以下に測定値から最適な直線y = axbの係数a とbを決定する手順を示す。 S = X (yi −axi −b)2 (残差の二乗和) ∂S ∂a = 2 X xi(axi b−yi) = 2 X (ax2 i bxi −xiyi) = 0 ∂S数 y = ax2 を考察する。その際、表、式、グラフを相互に関連付けながら、変化の割合やグラフの特徴など関数 ・学校図書(問い・y= ・グラフ→x,y の関係が比例かどうか?) ・教育出版(問い・グラフ→枚数が100 枚ときに何段?) ・大日本図書(コラムでの説明)




2次関数のグラフと直線
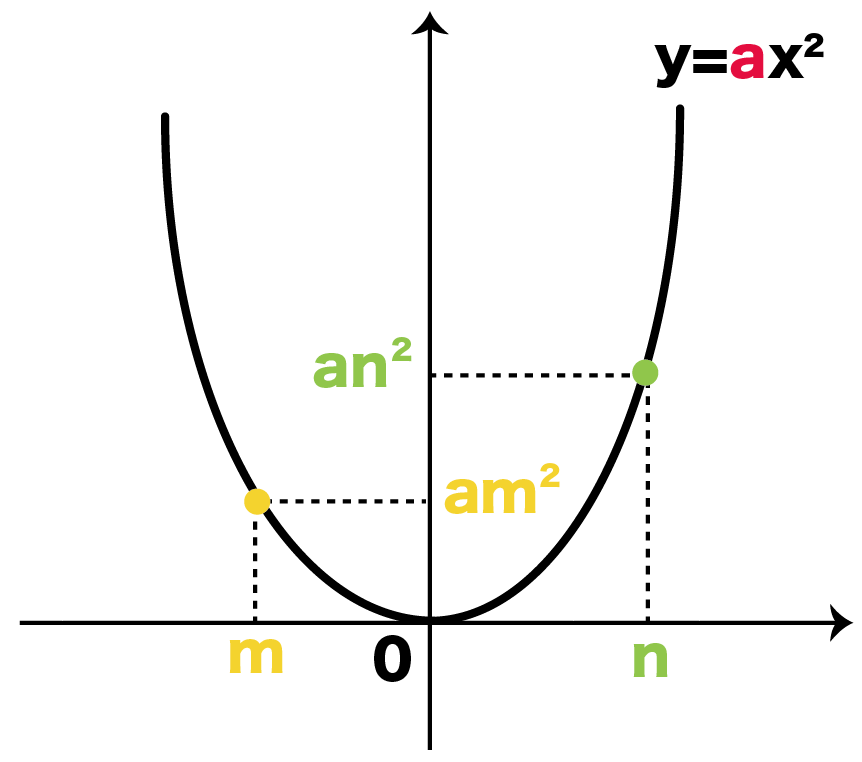



二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
\( y = ax b \) の値(今回は \( y = x \))が表示されている部分をクリックしてください。 すると、このようなウィンドウが右側に表示されています。 そこからカテゴリを「数値」もしくは「指数」を選んでください。Y=ax² の形になる、 「2乗に比例する関数」 でしか 使えない裏技なのですが、 (yの増加量)÷(xの増加量) よりも速いので、 基本を理解した人には オススメの公式なのです。 <ひとこと> なお、 (yの増加量)÷(xの増加量)LINEST関数による最小二乗法の計算 Excelには、最小二乗法による直線フィッティング用にLINESTという関数が用意されています。 一般的な使い方は =LINEST(計算に使うYの範囲、計算に使うXの範囲、Y切片を0にするかしないか) というような形式です。 X,Yという順番ではなく、Y,Xという順番であることに注意してください。 範囲の指定の方法ですが という表があり



Y Ax 2




高校数学 Y Ax 2 Bx Cのグラフ 練習編 映像授業のtry It トライイット
最小二乗法の計算は複雑でややこしいので、非常に助かりました。 3 1341 男 / 歳代 / 高校・専門・大学生・大学院生 / 役に立った / 使用目的 東京書籍中3教科書のp90〜116をまとめました。 学年 中学3年生, 教科書 新編 新しい数学3 東京書籍, 単元 関数y=ax^2, キーワード 関数ですから、y=ax² では、 ・"a"は「比例定数」とは呼べるが、 ・ 「変化の割合」とは言えない。 (⇒「変化の割合」は、 計算しないと分からない 。) こう言えるのです。 ちなみに、 「変化の割合」を求める式、 (yの増加量)÷(xの増加量)




Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト



1
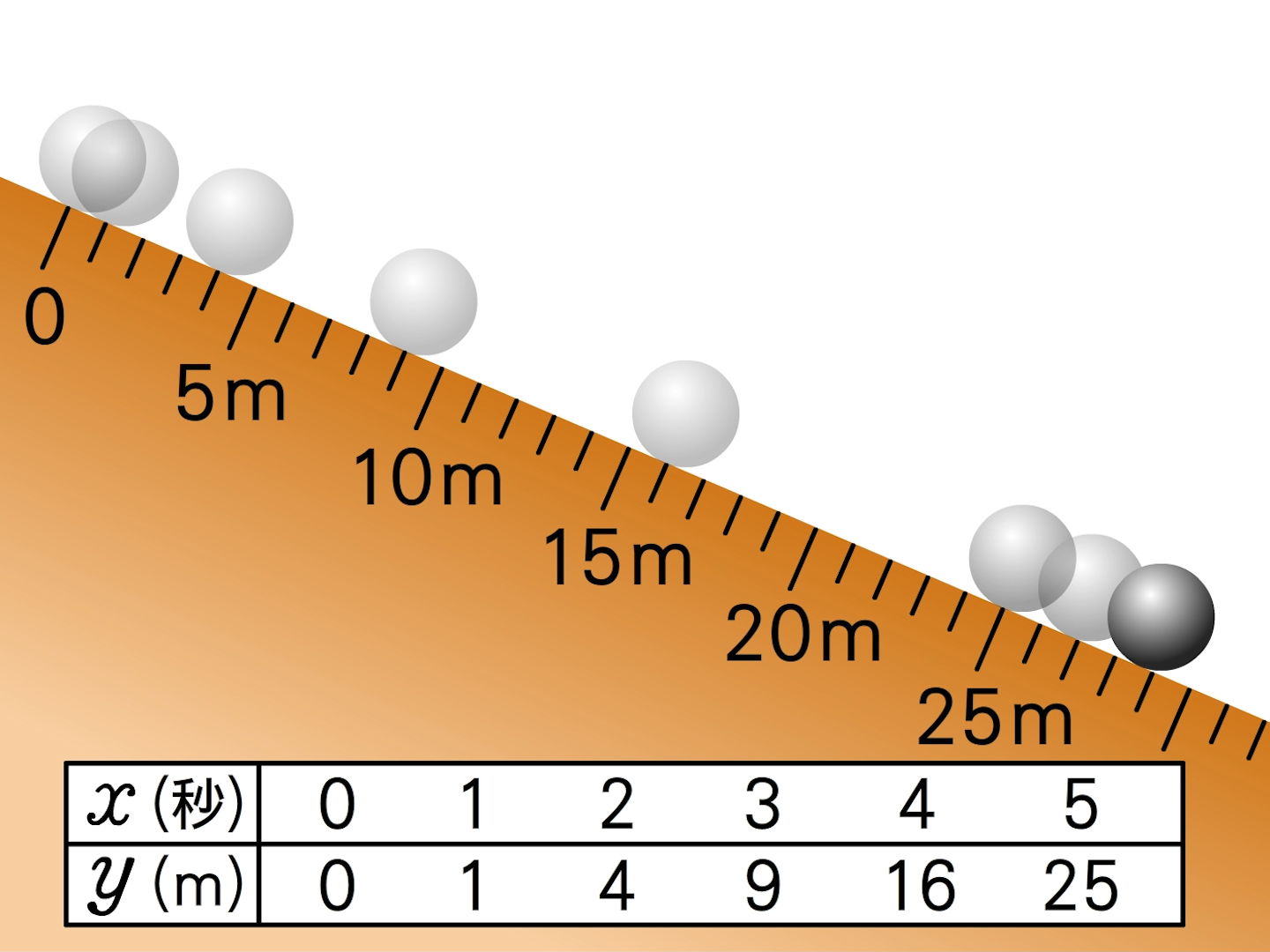
2次関数のグラフは,放物線とも呼ばれ,ボールを遠投したとき描く曲線のような形をしています。 その曲線を式で書くと,y=ax2 (a≠0) の形に書かれます。
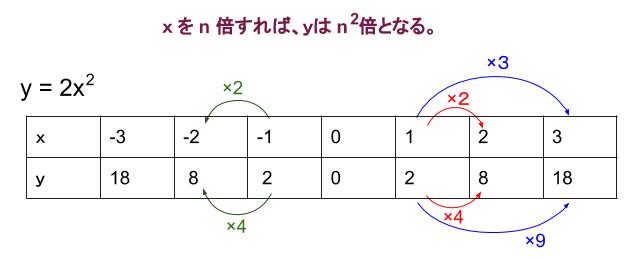



中学数学 Y Ax 2 2乗に比例 導入 中学数学の無料オンライン学習サイトchu Su



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf
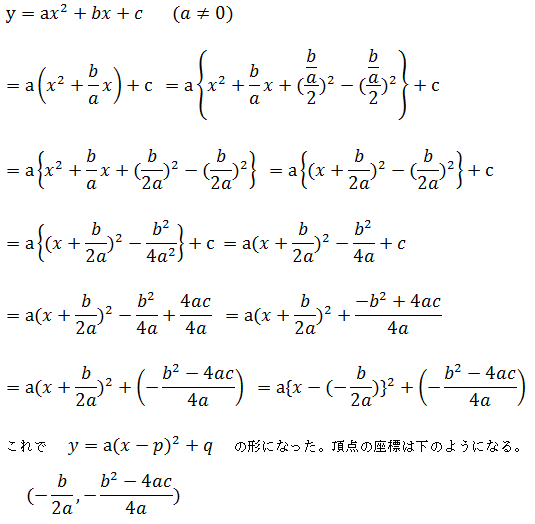



2次関数のグラフの平行移動 現代 Note




超簡単 二次不等式の解き方が誰でもわかる 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ




Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア




例題で学ぶ高校数学 Y Ax2 Q




二次関数 Wikipedia




ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download




高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月
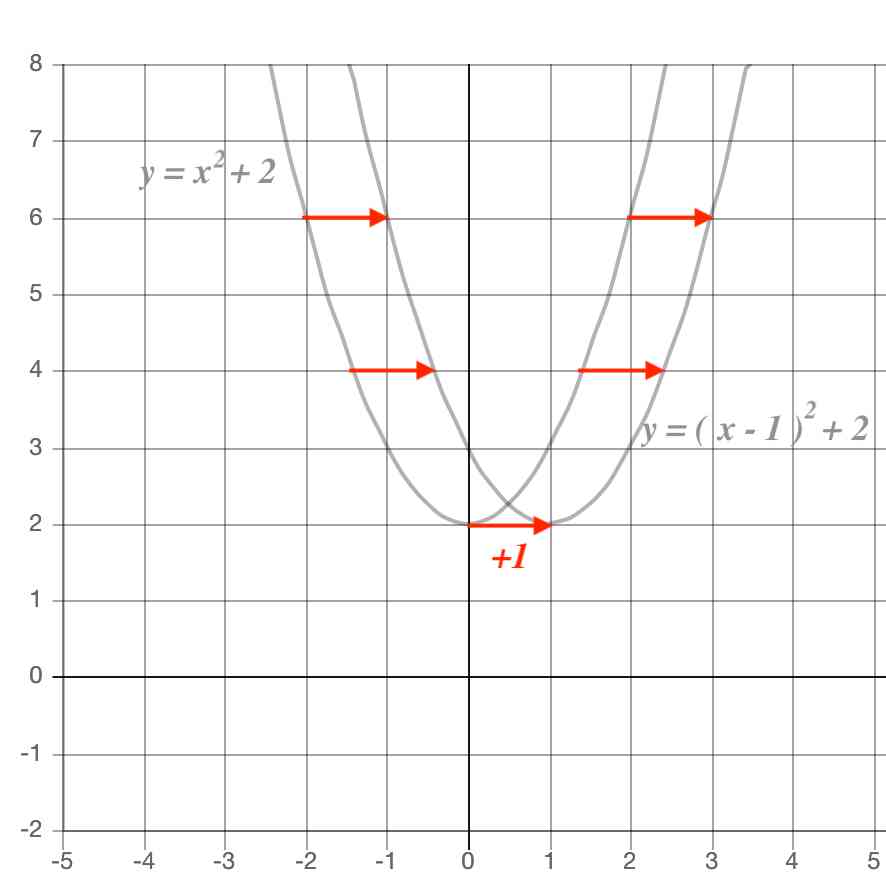



二次関数のグラフの書き方




Y Ax 2 Cのグラフ 数学i フリー教材開発コミュニティ Ftext
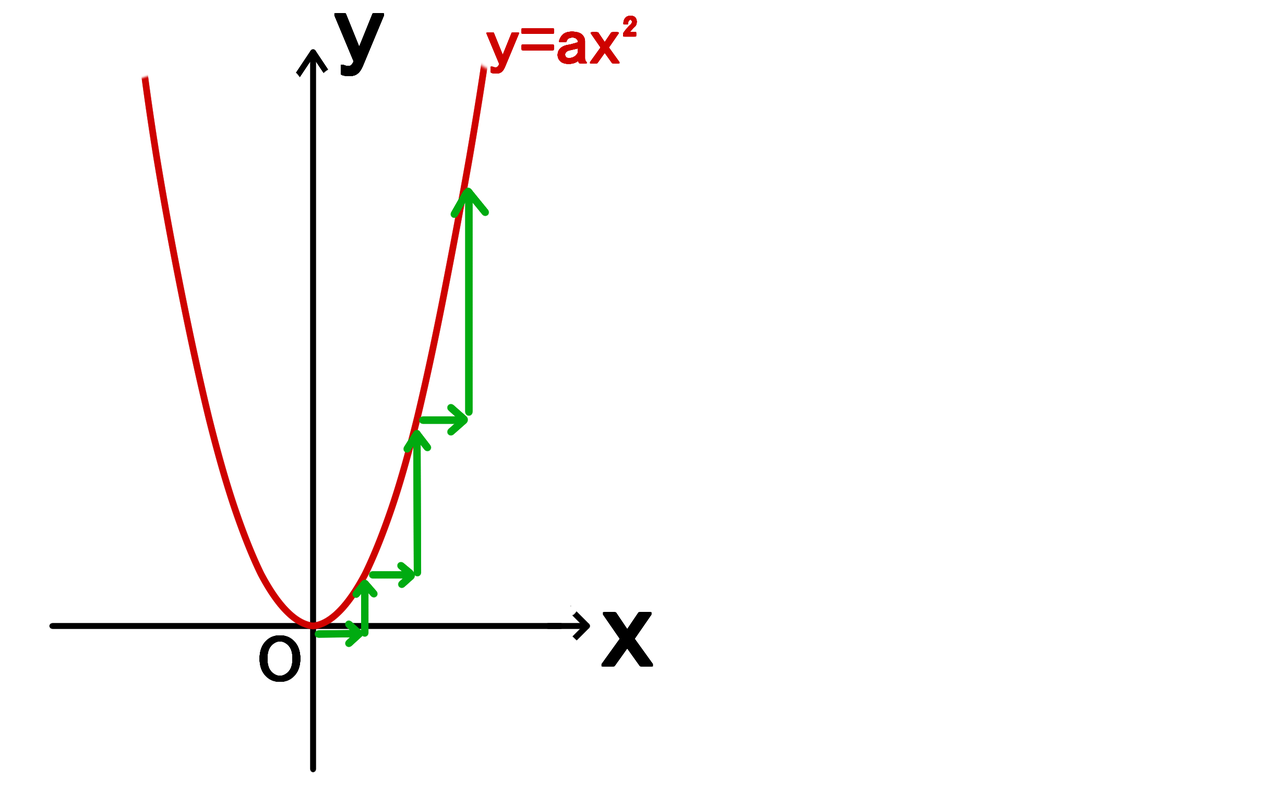



関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学



図は 関数y Ax二乗 のグラフと このグラフ上の2点a Bを Yahoo 知恵袋
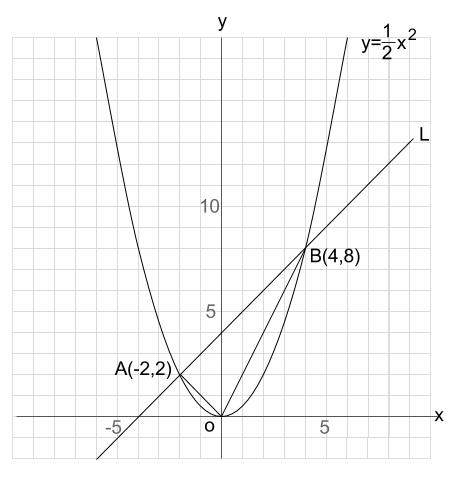



中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su




関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube




二次関数y ax 2 のグラフは点a 4 2 を通っている y線 数学 教えて Goo




yはxの二乗に比例する関数の問題 y ax 2とおこう 中学や高校の数学の計算問題




例題で学ぶ高校数学 Y Ax2




Y Ax 2 2次関数 のグラフ 高校入試 数学 良問 難問
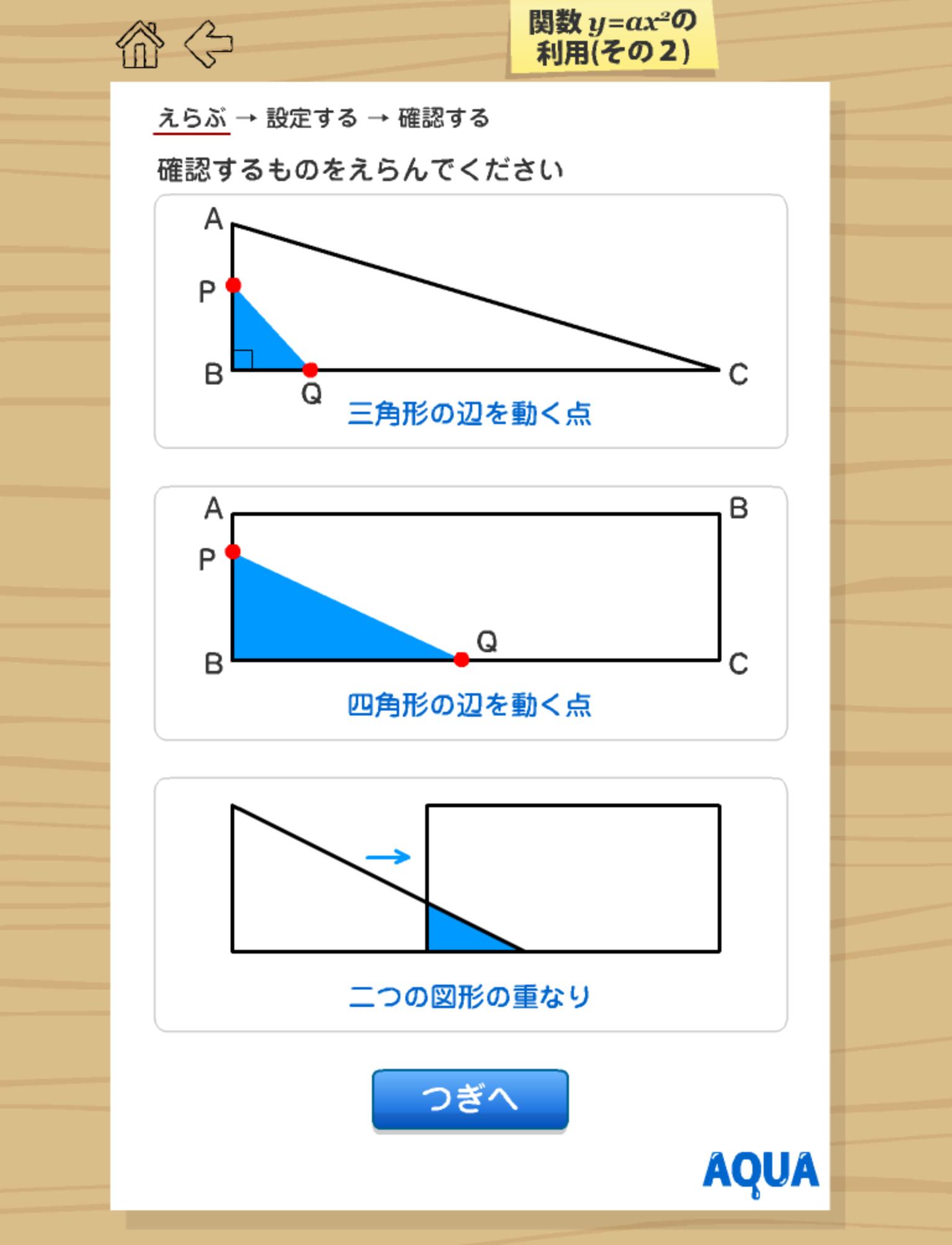



関数y Ax2の利用2 さわってうごく数学 Aquaアクア Fur Android Apk Herunterladen
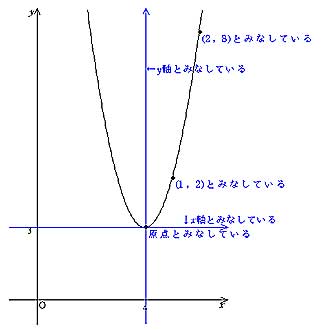



授業実践記録
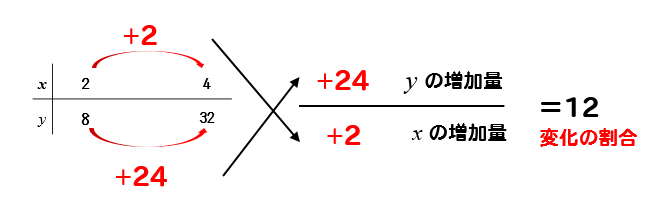



変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ




二次関数のグラフの問題 aの値で上か下かの向きが決まるよ 中学や高校の数学の計算問題




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中3数学 Y Ax 2のグラフ A 0 映像授業のtry It トライイット




関数y ax二乗 a 0 のグラフ上に3点a b cがあり それらの点のx座標はそれ Clear




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




Y Ax 2 グラフ Geogebra
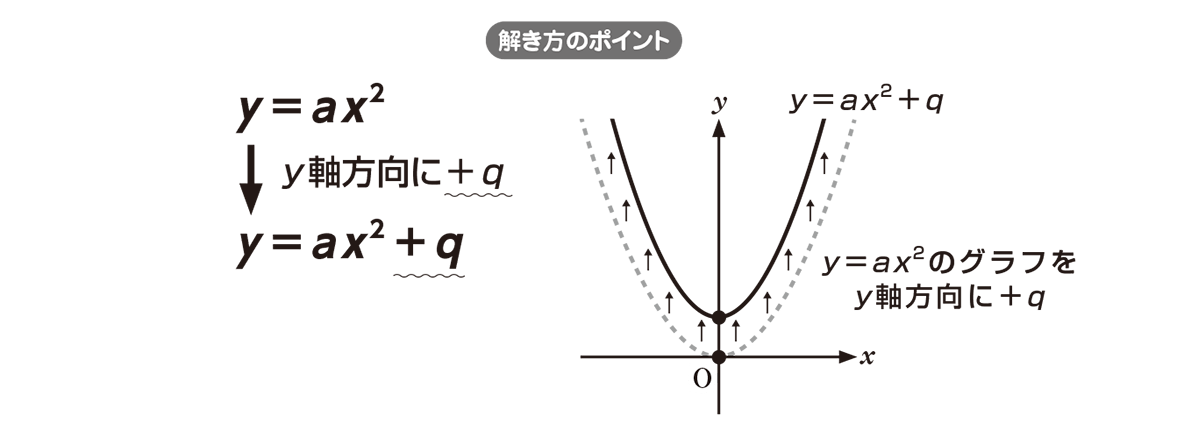



高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット




4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download




基本 二次関数y Ax 2 Qのグラフ なかけんの数学ノート
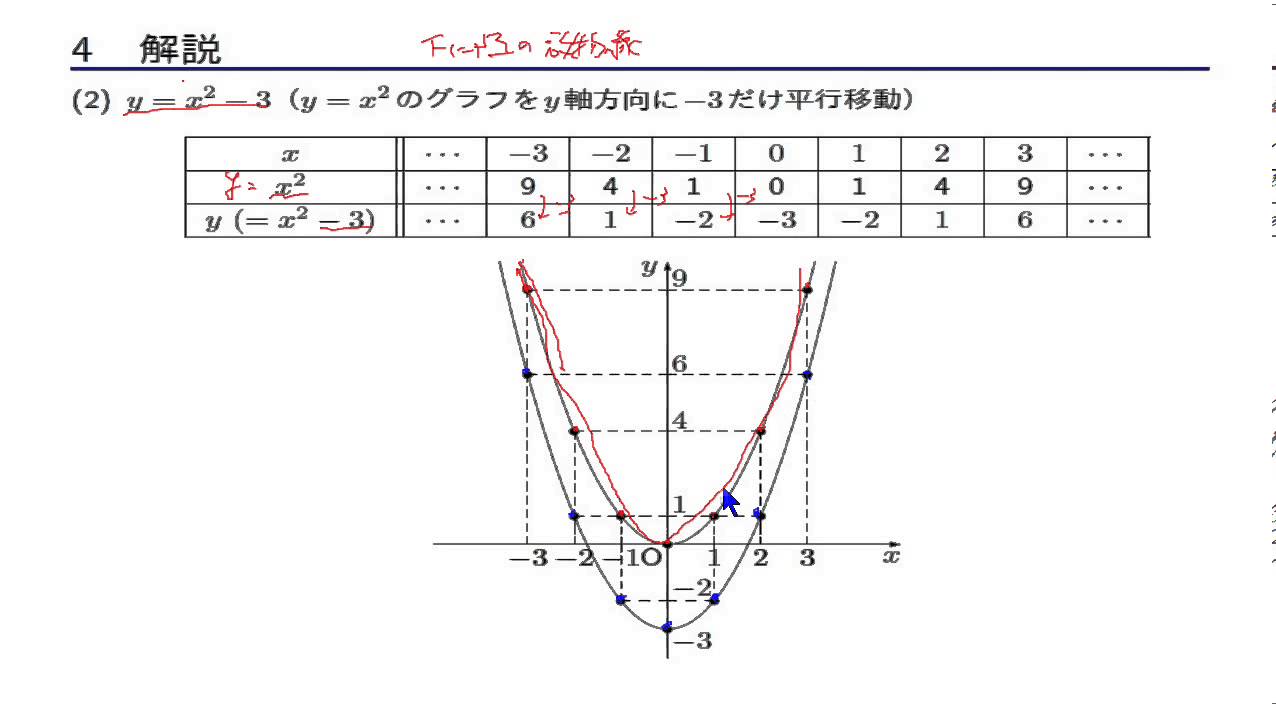



数学i 2次関数 2 2 Y Ax 2 Qのグラフ Youtube



Http Educom Sakura Ne Jp Wp2 Wp Content Uploads 17 06 Koum1 Pdf



1




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




Y Ax B 2x 1 1 のグラフが点 1 0 Okwave
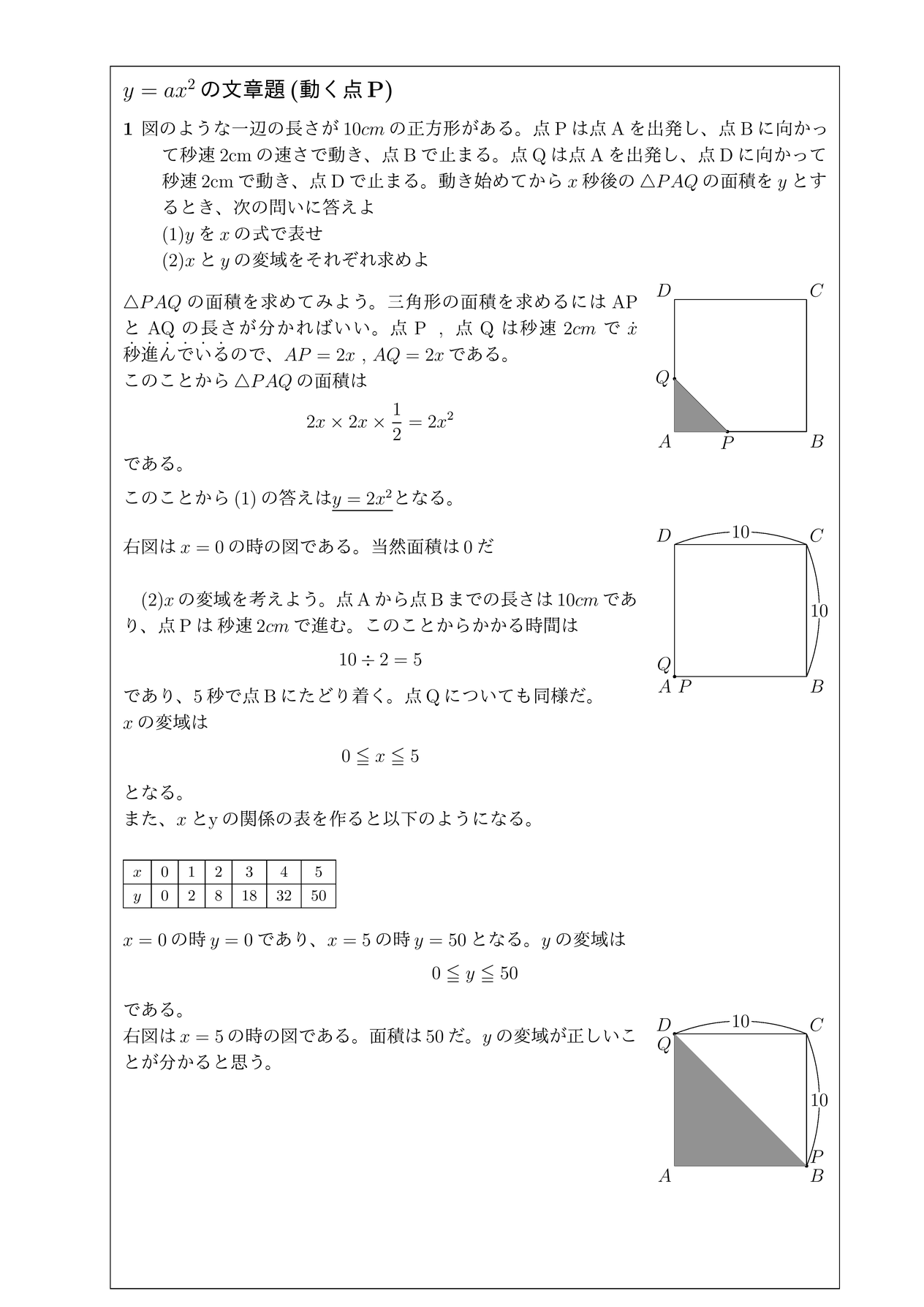



Y Ax 2を利用した文章題 チーム エン



2次関数のグラフと係数




Aは関数y Ax二乗のグラフと直線y 3分の2x 4との交点 Bは直線y 3分の2x Clear
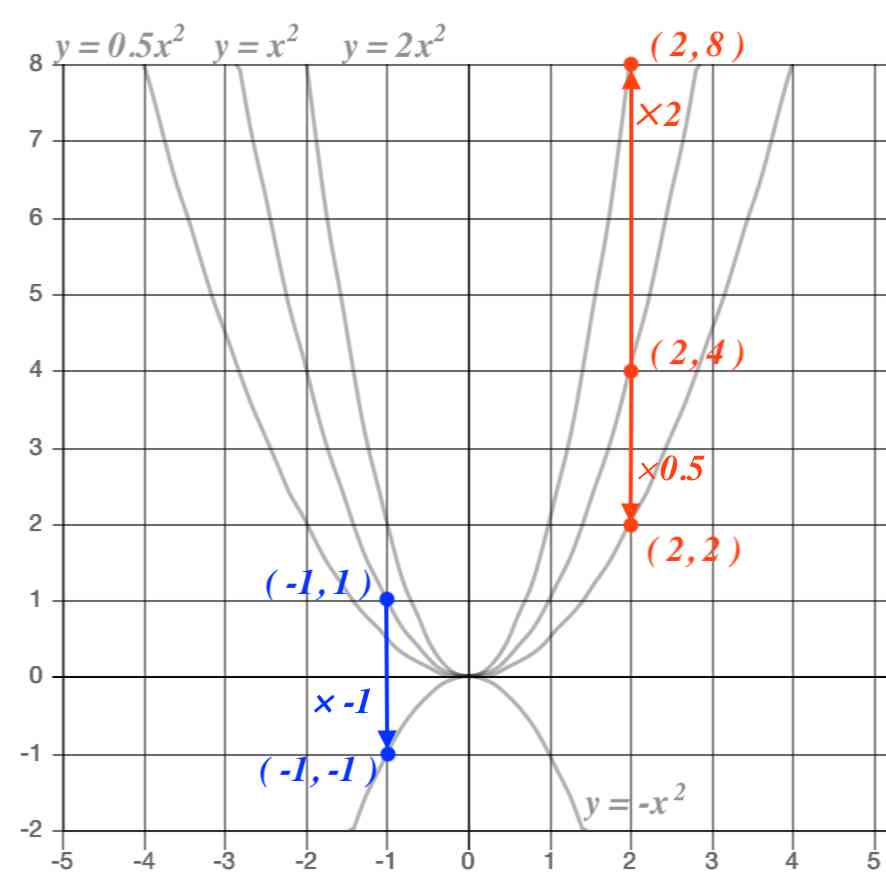



二次関数のグラフの書き方



数学の問題で Y Ax二乗 Bx Cの平方完成の仕方を教えて下さい Yahoo 知恵袋




2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント




Y Ax2乗 変域の求め方 変域から式を作る方法について解説 中学数学 理科の学習まとめサイト



図のように関数y Ax二乗 二次関数 のグラフ上に2点a Bがそれぞれの座標 Yahoo 知恵袋




中3 数学 y Xの二乗の値の変化 中学生 数学のノート Clear



数学3年 2次関数 Y Ax2 2次関数のグラフ 2次関数の変域 2次関数の応用 2次関数のグラフ Xの2乗に比例する関数 問題1 正解1 解説1 問題2 正解2 解説2 問題3 正解3 解説3 問題4 正解4 解説




中3 関数 Y Ax2 まとめ 中学生 数学のノート Clear



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく




関数y Ax2乗 変化の割合の裏ワザ公式 どうやって解くの Youtube




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext



画像 関数yax2乗 グラフ ニスヌーピー 壁紙




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット




Y Ax 2 Bx C のグラフのかき方 事後テスト解答例 Kyokuryo Math




中3 Y Ax二乗のグラフの性質 変域の求め方 中学生 数学のノート Clear




4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download



関数y Ax2のグラフ まなびの学園




2次関数のグラフ




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks
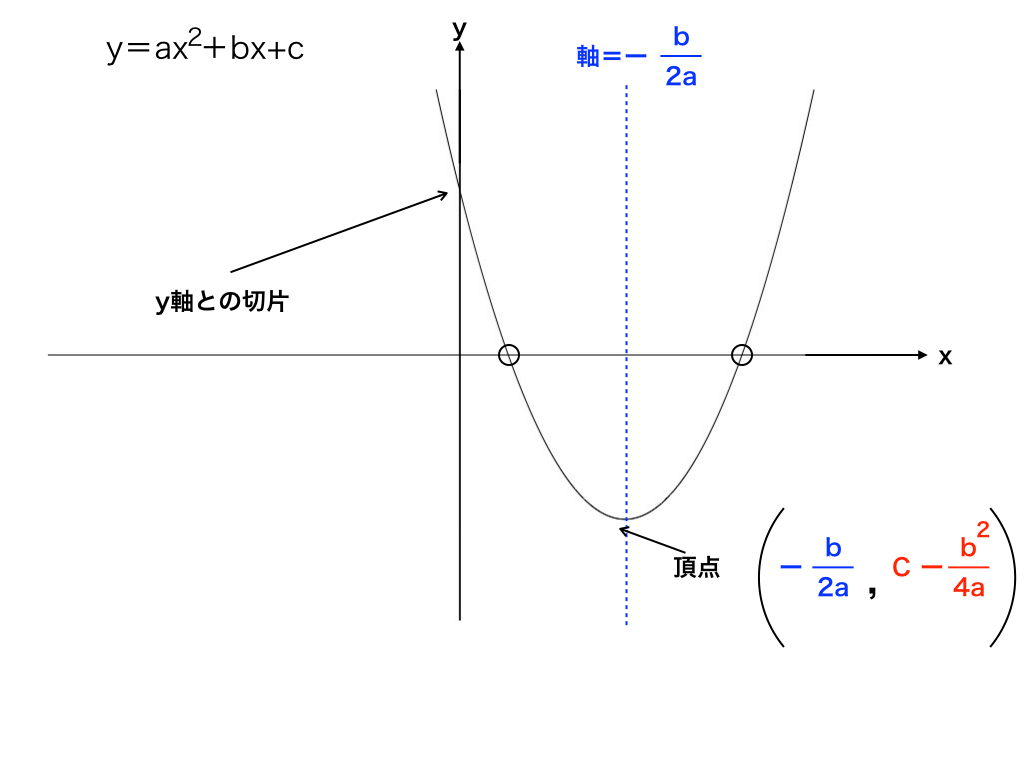



二次関数のグラフと解の存在範囲の問題をわかりやすく解説



中3数学 関数y ax二乗 放物線と直線1 発展問題 問題 324 プリント




なんで中学教科書では 関数y Ax2 を二次関数と呼ばないの Qikeru 学びを楽しくわかりやすく



中学数学 関数



関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは Youtube




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext




中3数学 Y Ax 2の増減 映像授業のtry It トライイット




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ



2乗に比例する関数 グラフ




中3 塾ノート 中3数学関数y Ax2乗 中学生 数学のノート Clear
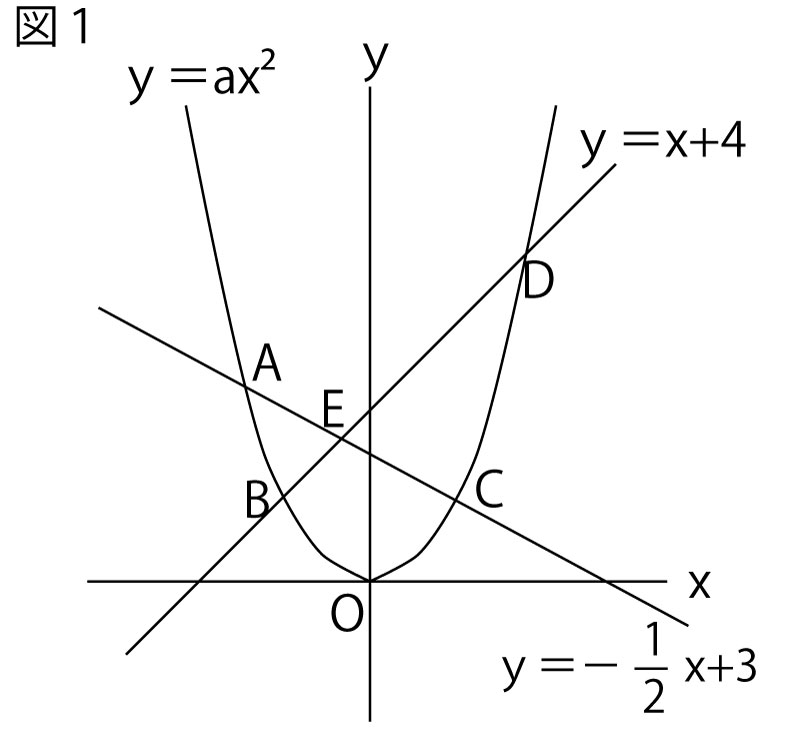



15年前期 千葉県公立高校入試 数学 第3問 二次関数 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



3年 関数 Y Ax 数学イメージ動画集 大日本図書



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf



2次関数y Ax Bx Cのグラフが次の図のようになるとき Yahoo 知恵袋




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット



1




Y Ax 2の変域 チーム エン



文字係数2次関数の頂点
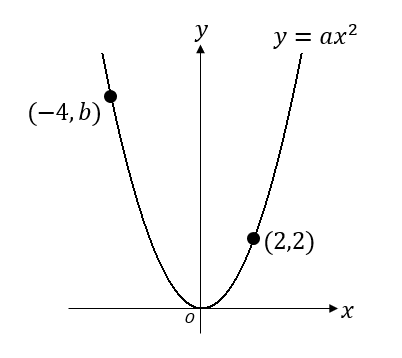



Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト



2次関数の各係数の意味



Y Ax 2



2次関数 中学 三角形の面積を二等分する直線の式 勉強ナビゲーター




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



3




二次関数 グラフの平行移動を具体例で詳細解説 式の仕組みから理解できます Rikeinvest



5 Yax2 Y2xb A Descubre Como Resolverlo En Qanda



中3数学 関数y ax二乗 変化の割合 発展問題 問題 322 プリント



0 件のコメント:
コメントを投稿