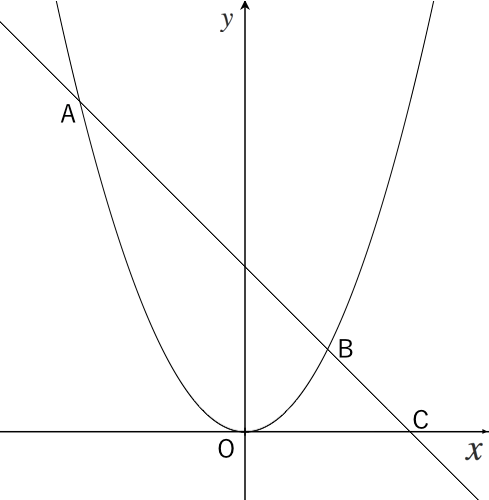
二次関数の利用 グラフ系の問題 苦手な数学を簡単に
一次関数1 一次関数の式 / 変化の割合 No.1 No.2 No.3 8 一次関数2 一次関数のグラフのかきかた No.1 No.2 No.3 9 一次関数3 一次関数の式の決定 No.1 No.2 No.3 10 一次関数4 二元一次方程式と一次関数 / 応用問題 / 動点の問題2年生 3 一次関数 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ③ 4 下の図の直線は,比例y =2x のグラフを表しています。 H このグラフのうち,x の変域を-1≦x
一次 関数 応用
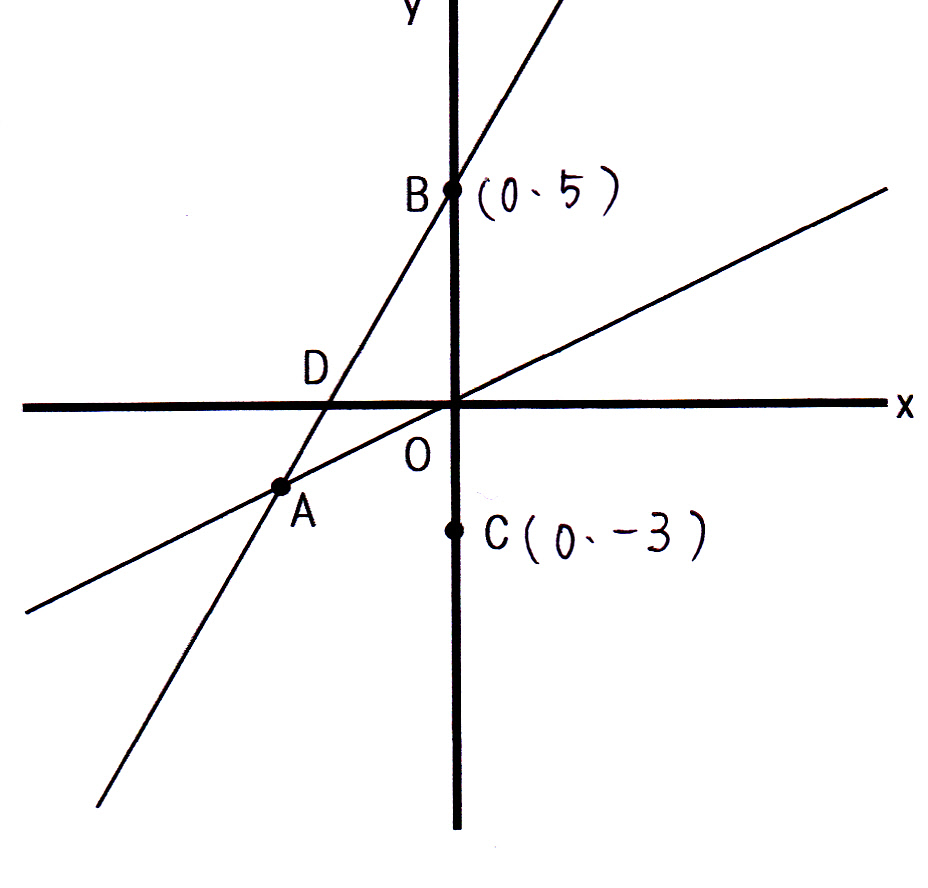
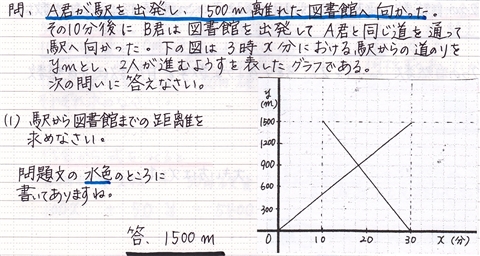
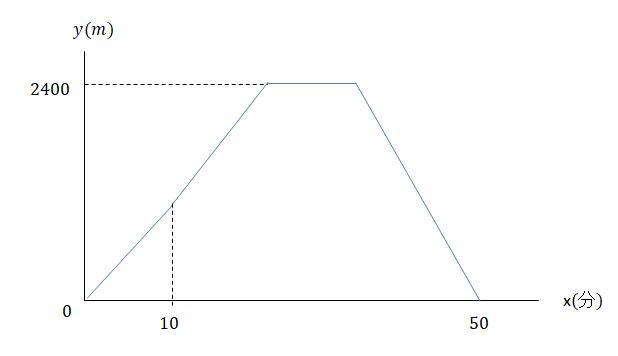
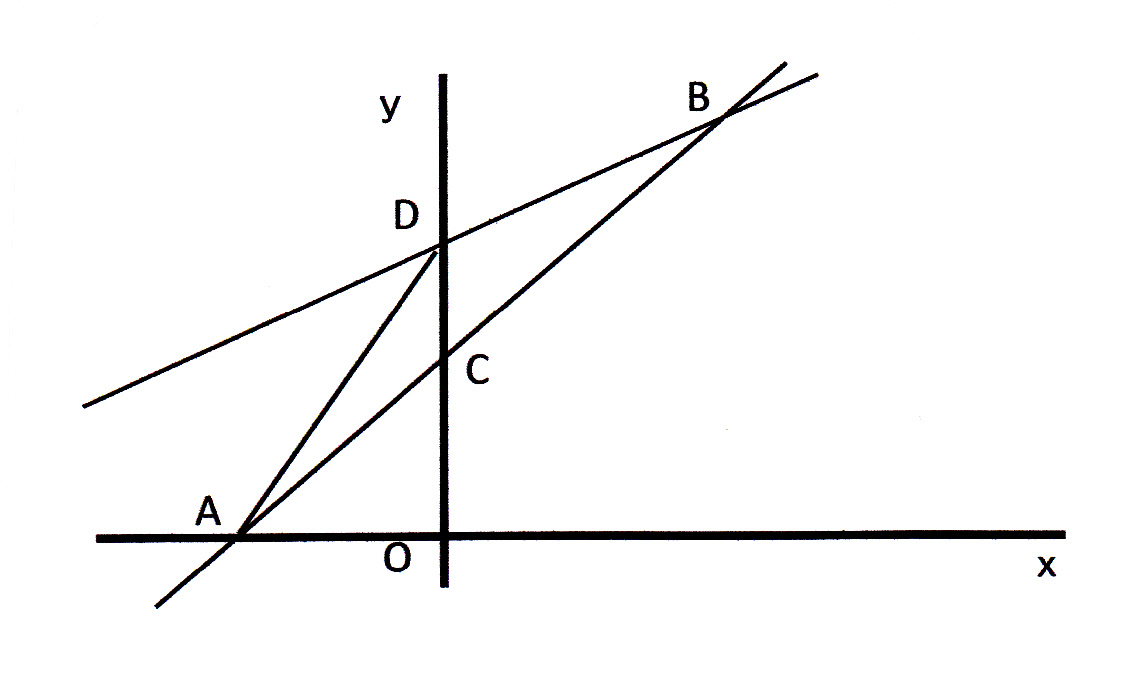
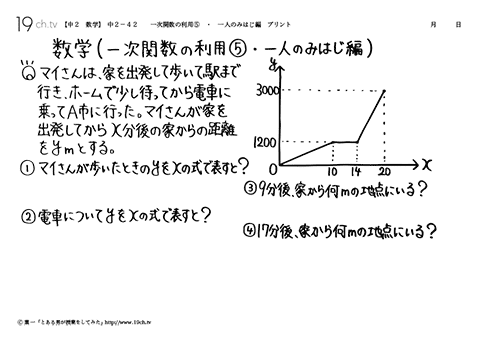
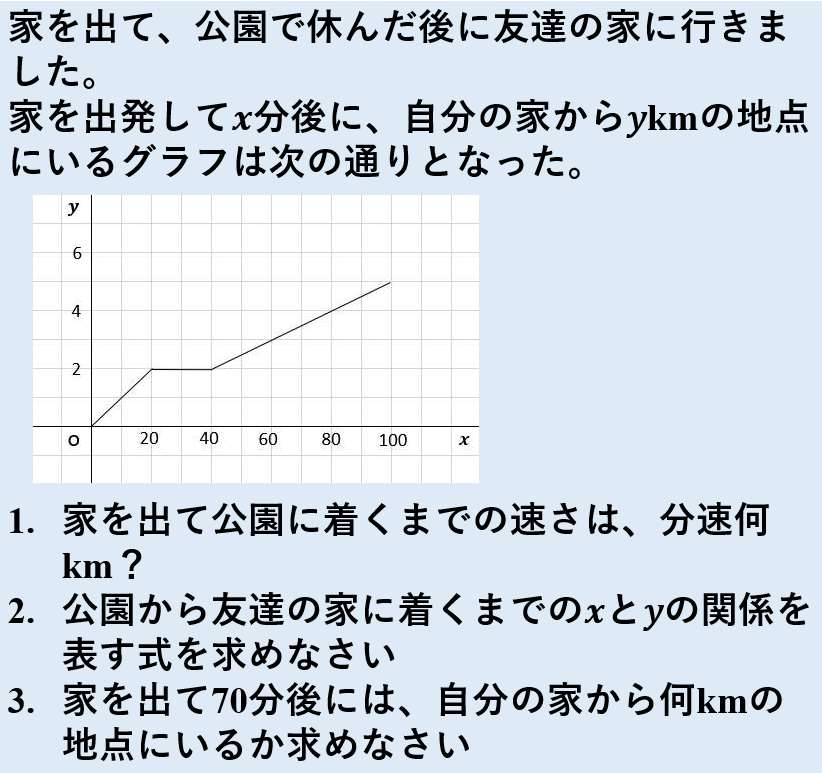
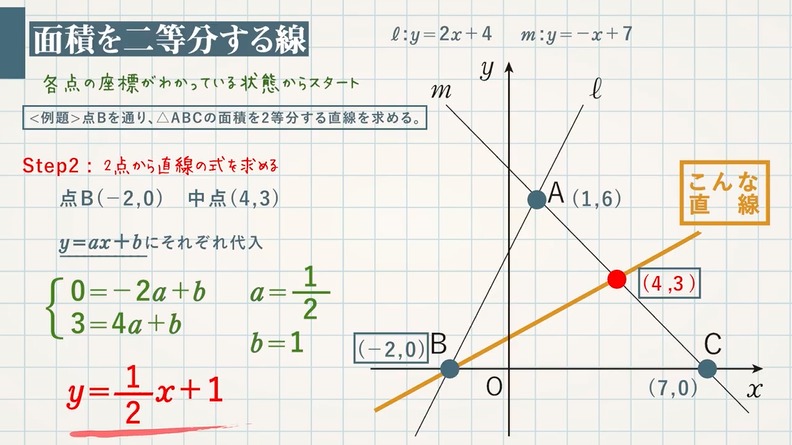
一次 関数 応用-一次関数で表された図形の面積とは? 一次関数はグラフに表したときに直線となります。 この一次関数が複数あると考えると、直線同士の交点や座標を使って図形が出来ることがあります。 解く方針としては、 直線の式を求める (直線の式が分からない 中2数学「一次関数の利用」の練習問題と解説です。距離のポイント 単位に気をつける。 x軸、y軸が何を表しているかチェック(単位は、速さ・距離・時間ともに、そのx、yにそろえる)点の移動のポイント グラフや表が用意されていない場合は、題意に沿
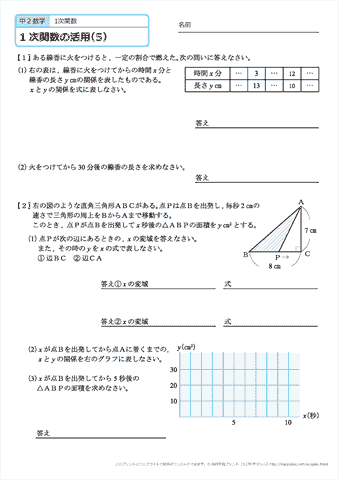
中学2年生 数学 1次関数の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
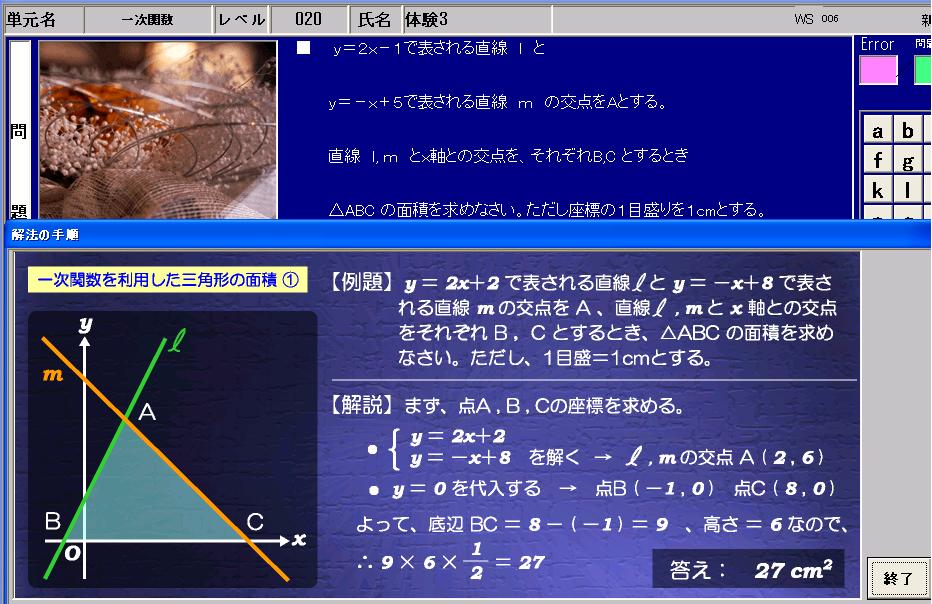
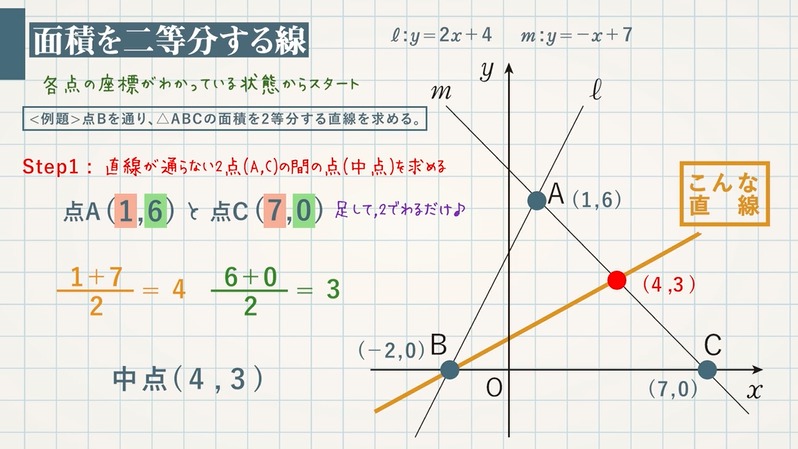
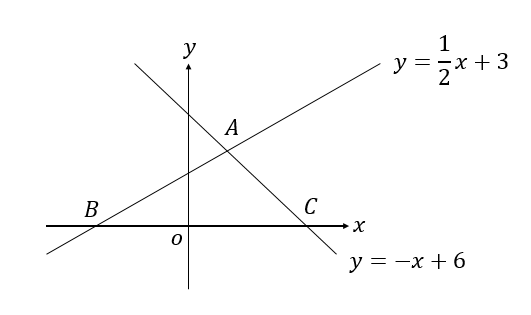
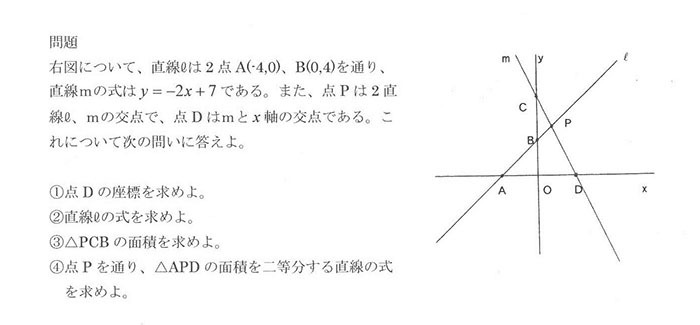
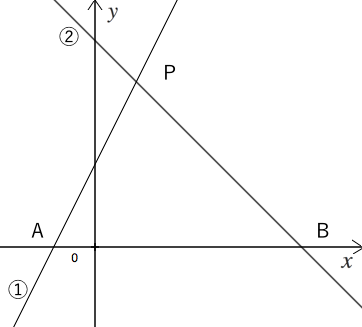
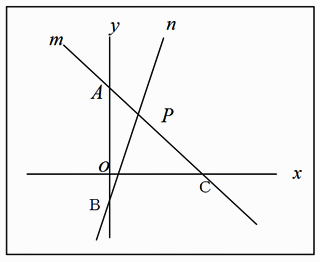
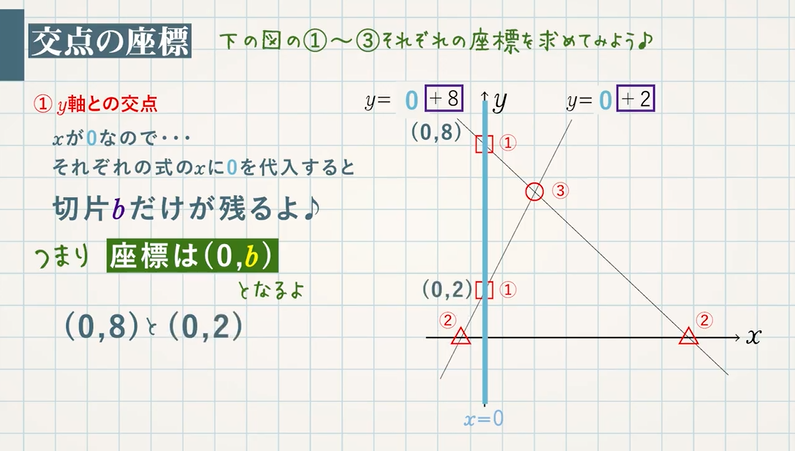
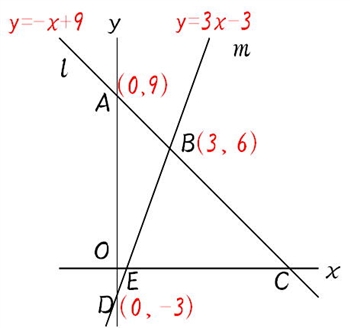
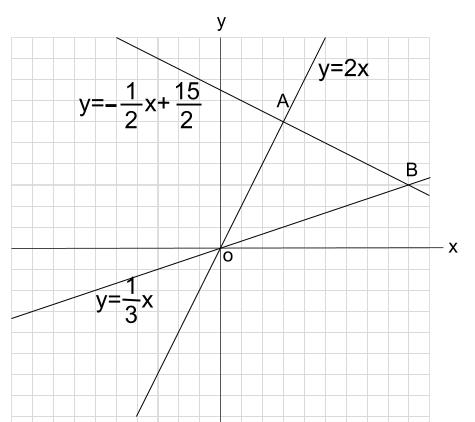
①1次関数と反比例,②2次関数,③動点p ①,1次関数,反比例グラフ ・最初の等積変形(★★☆☆☆)(オリジナル) 実は等積変形でなくても解けるのですが,まあ練習用に。 ・順序だてて(★★☆☆☆)(オリジナル) 関数記述対策の初めの方に。関数と図形 関数と図形2 直線と四角形 1次関数応用(動点) /1/7 2年一次関数総合問題Lv3 5(2) 点Pはlとx軸の交点(誤)→点Bはlとx軸の交点(正) 3年方程式文章題(割合2)3(1)解答 2番目の式 一次関数のグラフの利用1 一次関数の応用問題です。 入試にもよく出題されるので、しっかり学習してください。 いろいろな問題を解いていくことで、問題パターンに慣れていきましょう。 よく出る問題の解き方 例)直線ℓ y=2x6 直線m y=x+
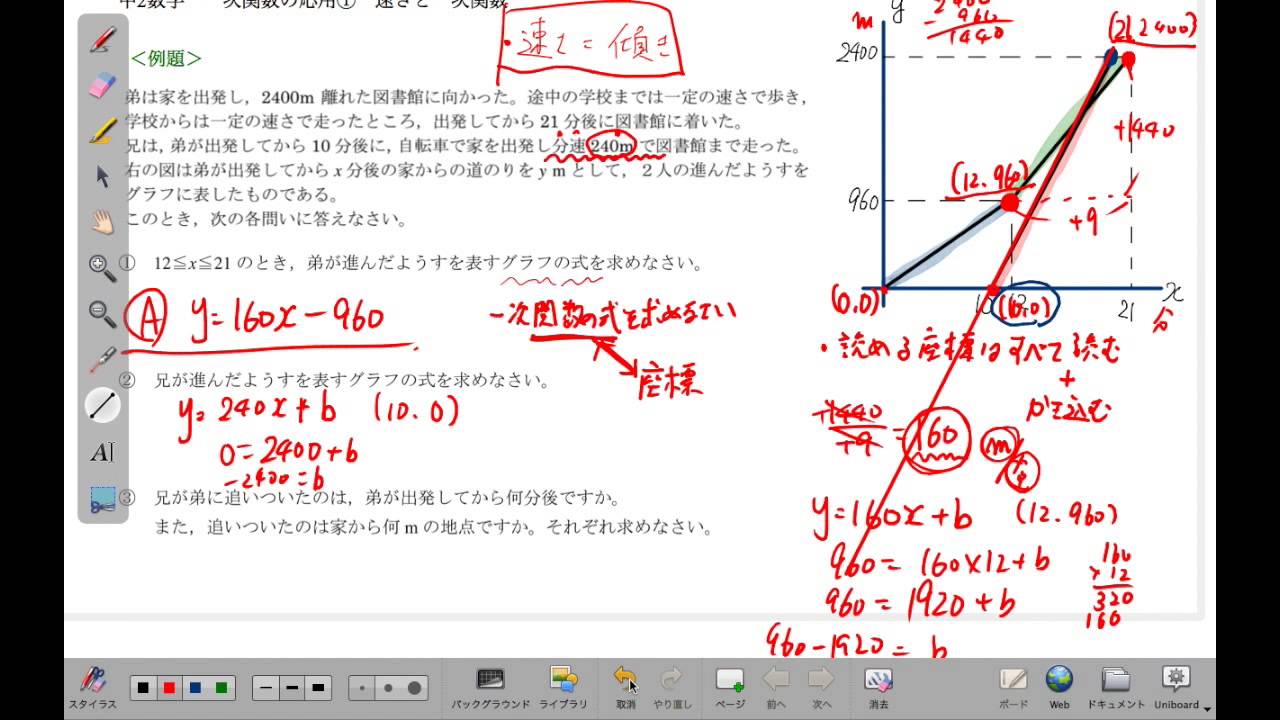
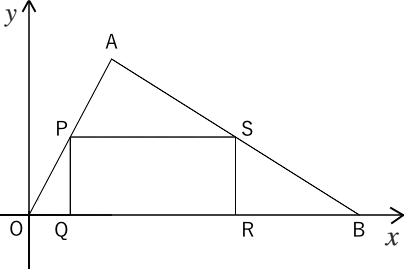
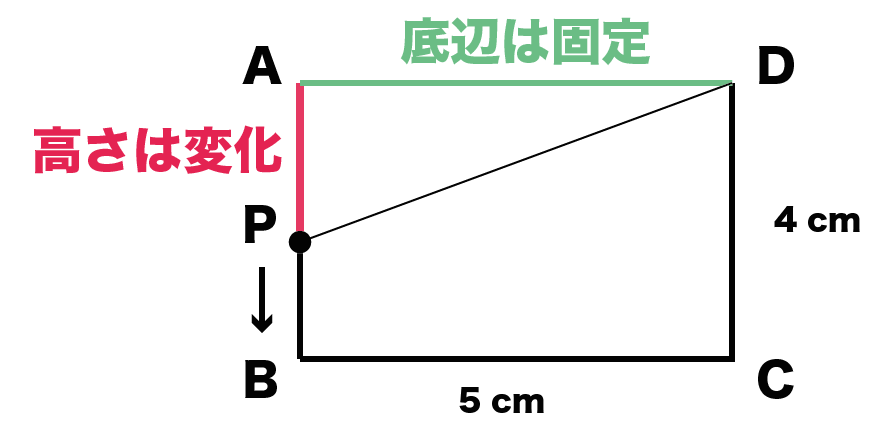
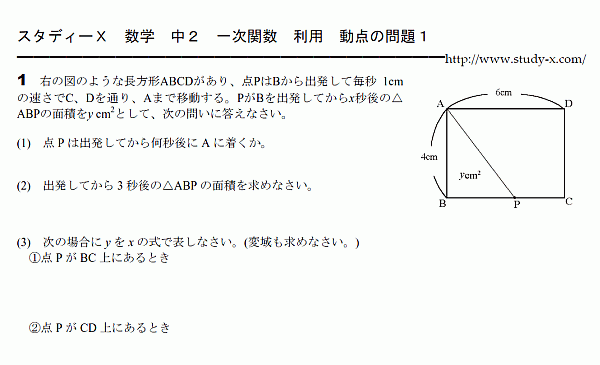
一次関数の利用の「動点」問題がわかる3つのステップ 問題のポイントは、 三角形の高さだけが変化していること だ。 逆に、底辺はどんなに時が経っても動かない。 高さの変化 をトラッキングすれば面積が計算できそうだね。 例題でいうと、 一次関数の傾き 傾きとは、文字通り「直線が(\(x\) 軸を基準に)どれだけ傾いているか」を指します。 一次関数は直線なので 傾きが一定で、必ず \(a\) の値 になります。 \(a\) が正の場合は右肩上がりの直線、負の場合は右肩下がりの直線になります。数学 一次関数利用 24K views Discover short videos related to 数学 一次関数利用 on TikTok Watch popular content from the following creators 夏せんせー夏ノ夜学🌻(@natchaan3), 楽しく勉強あきとんとん(@akitonton), gakuto(@g_y0330), 夏せんせー夏ノ夜学🌻(@natchaan3), ノーベル性科学ショー(@usagisex)
一次 関数 応用のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「一次 関数 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
なぜその生徒は「一次関数ってマジで意味わかんない!」から「二次関数の応用問題」を解けるように変化したのでしょうか? その理由を今回お話します。 この記事を読むといい人 一次関数で困っている人;一次関数の意味につい て関心を持ち,それらに ついて進んで探求しよう としている。 一次関数のグラフに関 心を持ち,特徴やかき方 を調べようとしている。 一次関数が実生活に深 く関わっていることに気 づき,問題の解決に利 用しようとしている。





0 件のコメント:
コメントを投稿